Algorithm - Ch2 動態規劃 Dynamic Programming

Chapter 2 動態規劃 Dynamic Programming

2.1 動態規劃簡介

動態規劃(Dynamic Programming)是指將一個較大的問題定義為較小的子問題組合，先處理較小的問題並將結果儲存起來(通常使用表格)，再進一步以較小問題的解逐步建構出較大問題的解。

動態規劃需合於 principle of optimality (Bellman 1957)
An optimal sequence of decisions has the property that whatever the initial state and decision are, the remaining decisions must constitute an optimal decision with regard to the state resulting from the first decision.

與其他演算法設計哲學比較

Divide-and-Conquer：Divide-and-Conquer 和 Dynamic Programming都是將問題切割再採用遞迴方式處理子問題，但是Divide-and-Conquer子問題的解通常不會重覆，重複時，通常會對相同子問題進行重覆計算，而不會像Dynamic Programming的子問題有大量的重複(overlap)，可以以table儲存不用再次計算，用空間換取時間。
Greedy Approach：Greedy Approach具有Selection Procedure，自某起始點開始在每一個階段逐一檢查每一個輸入是否適合加入答案中。如果所要處理的最佳化問題無法找到一個選擇程序來逐一檢查，而需要以一次考慮所有的可能情況的方式來處理，那就是屬於Dynamic Programming。因此若遇最佳化問題，先思考可否用Greedy Approach解，若不行再考慮Dynamic Programming。

2.2 經典動態規劃問題

Shortest path problem in weighted directed graph (negative edge allowed but no negative cycles)

定義：對多階段圖，求最短路徑
解法 (forward approach)

$f(k)$表示狀態 $k$ 到終點狀態的最短距離。
初始條件：$f(k) = 0$
遞迴式：$f(k-1) = min\{f(k)+W(k-1,k)\}，$其中$W(k-1,k)$表示狀態$k-1$到狀態$k$的距離

複雜度分析

時間複雜度 : $O( |V|+|E| )$
空間複雜度 : Table儲存$Cost_i(j)需O(|V|)$，但輸入Graph需$O( |V| + |E| )$

計算概念補充 : 對多階段圖求最短路徑有 forward approach 和 backward approach 兩種，以 forward approach 來說，遞迴式的展開方向 forward ，也就是$V_0 \rightarrow V_d$，但是解題時因為是用 bottom-up 的方式累積解答，所以數字要從$V_d$開始寫，一直累積到$V_0$結束。

Chained Matrix Multiplication Problem

定義：給定Matrix Chain : $A_1(d_0,d_1), A_2(d_1,d_2), ..., A_n(d_{n-1},d_n)$，求此Chain所需之乘法次數為最少之括號方式

$A_1(3,5)$表示第一個矩陣是3乘4的矩陣，注意$A$和$d$足碼之間的關係！
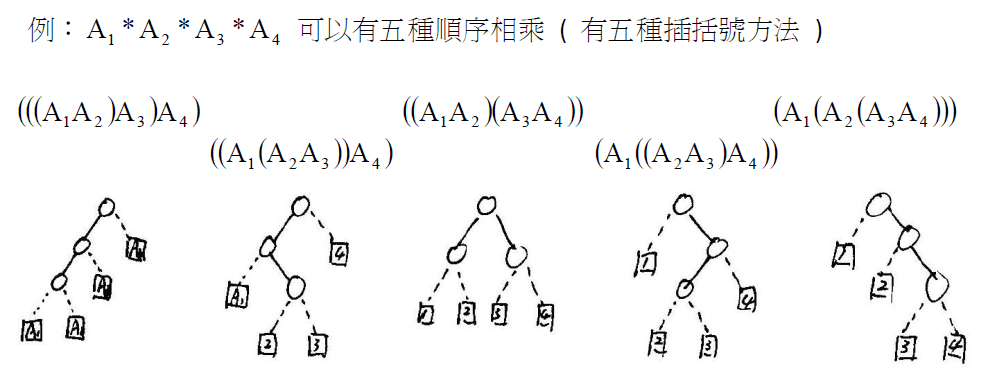
n 個 matrix 相乘有 $C_n = \frac{1}{n+1}{2n \choose n} = \frac{(2n)!}{(n+1)!n!}$ 種可能的配對組合，這個數很有名，又稱卡塔蘭數(Catalan number)。

解法

複雜度分析

空間複雜度 : 當$n$個矩陣會有約$\frac{n^2}{2}$個不同的子序列。
時間複雜度 : 可證明此一簡單的技術可使得運算時間由$O(2^n)$降至$O(n^3)$，使得其對實際應用有足夠的效率。

例題：$A_1(3×3)$,$ A_2(3×7), A_3(7×2), A_4(2×9), A_5(9×4)$, 求此五矩陣的最小乘法次數。
*要會把切割點表格(右下P表格)轉成實際的乘法順序，也就是乘法順序樹，再次提醒，注意$A$和$d$足碼之間的關係。

程式碼：

// Matrix Ai has dimension p[i-1] x p[i] for i = 1..n
MatrixChainOrder(int p[])
{
    // length[p] = n + 1
    n = p.length - 1;
    // m[i,j] = Minimum number of scalar multiplications (i.e., cost)
    // needed to compute the matrix A[i]A[i+1]...A[j] = A[i..j]
    // cost is zero when multiplying one matrix
    for (i = 1; i <= n; i++) 
       m[i,i] = 0;
 
    for (L=2; L<=n; L++) { // L is chain length
        for (i=1; i<=n-L+1; i++) {
            j = i+L-1;
            m[i,j] = MAXINT;
            for (k=i; k<=j-1; k++) {
                // q = cost/scalar multiplications
                q = m[i,k] + m[k+1,j] + p[i-1]*p[k]*p[j];
                if (q < m[i,j]) {
                    m[i,j] = q;
                    s[i,j]=k;  // s[i,j] = Second auxiliary table that stores k
                               // k      = Index that achieved optimal cost
 
                }
            }
        }
    }
}

The Longest Common Subsequence (LCS) Problem

定義：給定兩個Sequence $X = <x_1, x_2,..., x_m>$和$Y = <y_1, y_2,...,y_n>$,求$X$和$Y$所構成的最長共同子序列$LCS(X,Y) = Z = < z_1, z_2,..., z_k>$ 為何 ?

[注意] Substrings和Subsequences的差別

String：a segment of consecutive characters.
Sequence：need not be consecutive.

例如有一條字串(String) S = "a t g a t g c a a t"，則
Substrings of S : "g a t g c" , "t g c a a t"
Subsequences of S : "a g g t" , "a a a a"

解法

若 $i$ 或 $j$ 為 $0$，表示 $X$ 或 $Y$ 這兩條序列的其中一條為空序列。
若 $x_i = y_j$ ，則$c[i,j]$所表示的序列長度,是由$<x_1,x_2,...,x_{i-1}>$和$<y_1,y_2,..., y_{j-1}>$兩序列所構成之最長共同子序列的長度，即$c[i-1, j-1]$)再加上1。
若 $x_i \neq y_j$，則$c[i, j]$的序列長度是由下列兩個不同的最長共同子序列長度當中之最大值所構成：

$<x_1, x_2, ..., x_{i-1}>$ 和 $<y_1, y_2, ..., y_j>$ 兩序列所構成之最長共同子序列的長度$c[i-1, j]$
$<x_1, x_2, ..., x_i>$ 和 $<y_1, y_2, ..., y_{j-1}>$ 兩序列所構成之最長共同子序列的長度$c[i, j-1]$

例題：shows the tables produced by LCS-LENGTH on the sequences X = 〈A, B, C, B, D, A, B〉 and Y = 〈B, D, C, A, B, A〉. The running time of the procedure is $O(mn)$, since each table entry takes $O(1)$ time to compute.

LCS的應用

Longest increasing subsequence

Y ← Sort(X); //Y具有遞增性
Z ← LCS(X, Y); //找出X與Y間的最長共同子序列且具有遞增性

Longest common substring：計算連續的「左上箭頭」有多長

c[i, j] = 1 + c[i-1,j-1] ,if x=y
= 0 ,otherwise

0/1 Knapsack problem

定義：有 $n$ 種物品，物品 $j$ 的重量為$w_j$價格為$p_j$。我們假定所有物品的重量和價格都是非負的。背包所能承受的最大重量為$W$。如果限定每種物品只能選或不選(0或1)，在總重量不超過$W$的前提下，我們希望總價格最高，則此問題稱為0/1背包問題。
解法：我們將在總重量不超過$Y$的前提下，總價格所能達到的最高值定義為$A(Y)$。$A(W)$即為問題的答案。$A(j, Y)$的遞推關係為：

$A(0, Y) = 0$
$A(j, 0) = 0$
$w_j > Y, A(j, Y) = A(j - 1, Y)$
$w_j ≦ Y, A(j, Y) = max \{ A(j - 1, Y), p_j + A(j - 1, Y - w_j) \}$

通過計算$A(n, W)$即得到最終結果。
3.的意思是，第$j$項物品根本拿不起來。
4.的意思是，要維持原本拿的東西，或是放下其中一樣東西拿起新的第$j$項物品。

複雜度分析 : 時間和空間皆為$O(nW)$。若重量剛好為順序資料，則時間複雜度為 $O(n^2)$，空間複雜度為 $O(n)$。
重要概念 : 儘管背包問題的時間複雜度為$O(nW)$，但它仍然是一個NP完全問題。這是因為一般化的重量$W$相對於整個問題的輸入大小並不成線性關係，而是$logW$(也就是$W$表示成binary所需要的bit數)。因此整個演算法針對input size的複雜度為$O(n \times 2^{logW}) = O(n \times 2^n)$。
例題：Item = {weight, value}，C = [{4,5},{2,5},{6,2},{5,4},{3,3},{5,4},{2,3},{5,7}]

另外一種背包問題，Fractional Knapsack Problem，物品可切割的情況，則可用Greedy algorithm求解，因為一直選取區域最佳解可以構成全域最佳解。

[註] 其他的經典動態規劃問題

Optimal binary search tree：見資料結構 Advanced Tree
Bellman-Ford algorithm for Single sourse shortest paths：見演算法 Graph Algorithm
Floyd's algorithm for All-pairs shortest-path：見演算法 Graph Algorithm

Pages

2015年1月23日星期五