Formal Language - Ch2 非決定性有限自動機 Nondeterminism Finite automata, NFA

非決定性有限自動機(Nondeterminism Finite automata, NFA)定義
一個非決定性有限自動機是含有5個元素的 5-tuple$(Q,Σ,δ,q_0,F)$ ，意義分別是 (狀態集$Q$, 字母集$Σ$, 轉移函式$δ$, 開始狀態$q_0$, 結束狀態$F$) ，從定義中可知F可以是空集合，表示沒有可以接受的狀態。


原文定義如下：
A finite automaton is a 5-tuple $(Q,Σ,δ,q_0,F)$ , where

1. $Q$ : is a finite set called the states
2. $Σ$ : is a finite set called the alphabet
3. $δ$ : $Q \times Σ_\varepsilon \rightarrow P(Q)$, is the transition function //箭頭線段代表狀態的變化
4. $q_0 ∈ Q$ : is the start state //開始狀態
5. $F ⊆ Q$ : is the set of accept states or final states //接受狀態

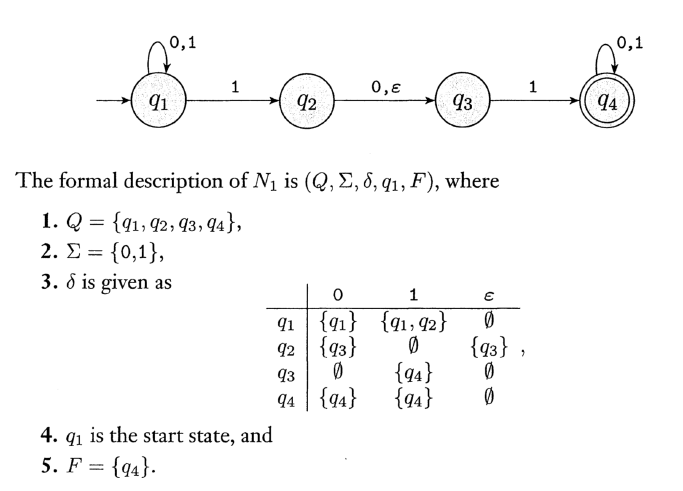
看一個狀態圖例子最容易理解：

[用心去感覺] DFA和NFA的不同之處

重點是定義3.的轉移函式

• 可不消耗($Σ_\varepsilon$)字串換狀態， 所以可能有剪頭可以自動轉移不用吃字元。
• 型別變成集合(冪集，power set)，因為DFA同時走很多條路
• 注意在追蹤狀態時，是同時走多條路，其中一條路接受就接受，有點平行計算的感覺，不是選擇也不是機率。
• NFA下的「計算」定義類似，注意事項亦相同。

DFA和NFA等價 (Equivalence of DFAs and NFAs)

Theorem : Every NFA has an equivalent DFA

我們要證明NFA和DFA等價，也就是任找一個NFA我們都可以找到一個DFA使兩者recognize的language相同，反之亦然。

DFA to NFA : 顯然成立，把轉移函式改一下型別即可。

DFA to NFA : 改寫方式如下

1. 狀態集 : $Q' = P(Q)$，取power set。
2. 轉移函式 : $\delta(R,a) = \bigcup_{r \in R}  \delta(r,a)$
3. 起始狀態 : $q_0' = \{q_0\}$
4. 結束狀態 : $F' = \{R \in Q'\ |\ R\ contain\ an\ accept\ state\ of\ N\ \} $

*$\varepsilon$處理 : 把可以走到的加進去set中，例如有a-d路徑，則{a,b}變成{a,b,d}

下面有一個實際的例子 : 

Regular Operations正確性證明

因為證明出DFA = NFA，因此可以使用NFA來證明DFA各種operation是可行的。

Reference

交大陳穎平教授正規語言講義